有名な「なんとかの三角形」を集めてみた
2022/04/13
有名な“なんとかの三角形”をまとめてみた。三角形なのに5つなのはご愛嬌ということで。
パスカルの三角形
パスカルが1654年に発表した三角形。『パンセ』において「人間は考える葦である」と言ったあのパスカルです。
を計算（二項展開）したときの各項の係数（二項係数）を三角状に順次並べたもの。上の頂点に1を置き、左右隣り合った数の和をその間の下段に置いていくとできあがる。
2行目には自然数（1,2,3,4,5,…）が、3行目には三角数（1,3,6,10,15,…）が現れたり、ちょっと見方を変えるとフィボナッチ数が現れたりと、深遠なる数理が潜んでいるらしい。
そんなことはさて置いても、「 
を展開せよ」なんて問題がテストに出たときは、この三角形を使えばわざわざ6回掛ける必要もなく、チャチャッと答え
（ 
）
を導くことができる。便利です。
カニッツァの三角形
イタリアの心理学者ガエタノ・カニッツァが1955年に発表した錯視図形。一部を欠いた円をうまい具合に並べると、その中に存在しない白い正三角形が見える。
さっきは「存在しない」三角形と言ったけれど、見えるのなら「存在する」と言ってもあながち間違いではない。ややこしい。
また、このような現象を、「ないものが見えるとは、脳はなんてすごいんだろう」と捉えるか、「ないものが見えてしまうなんて、脳っていい加減だよね」と捉えるか悩ましいところ。水が半分入ったコップをどう捉えるかと同じように、人それぞれの気質が表れるのかもしれない。
ルーローの三角形
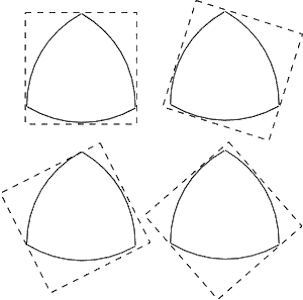
ドイツの機械工学者フランツ・ルーローが開発した三角形。正三角形の各頂点を中心に、半径が正三角形の1辺となる円弧をコンパスで描けばできあがる。図形の幅どこをとっても同じ長さとなる定幅図形の一つ（最もポピュラーな定幅図形は円）。
おじさんたちにはマツダのロータリーエンジンと言えばすぐに頭に浮かぶ図形。正方形の内側にピタリと接しながらクルクル回すことができる。ただこうやって回すと三角形の中心はじっとしていないので、うまく回すのはかなり難しそう。機械技術屋の腕の見せ所だったろう。
また、この形でできたドリル歯を使うと正方形の穴を掘ることができる。このときも中心が固定されていないので、普通のドリルと違う軸の工夫が要る。
ペンローズの三角形
数学者ロジャー・ペンローズが考案した不可能図形。四角柱が3本直角に組み合わされているにもかかわらず、全体として三角形になっている、紙の上には描けるけど立体としてはありえない図形。エッシャーの作品群にも影響を与えたらしい。
3次元ではありえないはずなのだが、でも実際に作っちゃってる人たちはいる。あたかも「そう見える」ということだけれど。
上のはだいたい予想つくけど、下のは想像の範囲を超えています。。
なお、このペンローズさん、「ペンローズ・タイル」なんて美しいタイル（平面を隙間なく埋め尽くす方法）も考案している。そして真の姿はすごい物理学者なのです。
シェルピンスキーの三角形
フラクタル図形のひとつ。自己相似性があり、どこまで細かく見ていっても同じ図形が現れてくる。シェルピンスキーが1915年に考えた。
- まず、正三角形を1つ考える。
- 正三角形の3つの辺の中点を結んでできる正三角形を取り除く。
- 残った3つの正三角形について、2と同じ操作をする。
- 残った9つの正三角形について、2と同じ操作をする。
この操作を永遠に（無限回）繰り返してできる図形がシェルピンスキーの三角形。シェルピンスキーのギャスケットとも呼ばれる。
この図形の線の長さは無限大、面積は0。ようするに、ある限られた領域に無限長の線が詰め込まれている（線なのでもちろん面積はない）ということで、そんなこと言われると頭がクラクラしてくる。フラクタル図形の不思議さというか、無限の不思議さを味わわせてくれる三角形なのです。