山の高さを測る

新田次郎は『劒岳＜点の記＞』で、陸地測量部の測量官、柴崎芳太郎が明治40年当時未踏峰とされていた剱岳の測量に挑む姿を描いた。嵐、雪崩など苛烈な自然と闘いながらの命がけの測量であった。。山の位置や標高を真摯に測定しようとすれば並々ならぬ覚悟が要るということだ。

とは言っても、そうそう命がけにはなれないので、もう少し手軽に山の高さを測りたい。そんなのiPhoneのコンパスで一発じゃん、てのはなしね。ここではGPSなんかもないものとする。

低くて小さい山ならレベル（水準儀）を用いて小刻みに高低差を計測してもよいのだが（直接水準測量）、しんどい。

もっと効率的に、なおかつ精度良く測るには三角形、三角関数を使う。

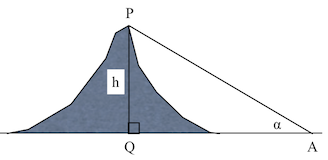
一番単純なのは図1の場合。山を見上げて水平との角度αを測る。山の頂点をP、山から離れた点をA、Pから垂線をおろしてAと同じ高さで交わった点をQとすると、山の高さhは、

   

で求まる（三角水準測量）。

この山までの距離APやAQがわかればいいのだが、一筋縄ではわからない。まあレーザー――トータルステーション、光波測距儀（コウハソッキョギ、どこかの拳法の奥義のようなひびき）なんか――を使えばAPは測れるけれど、それでも頂上に反射体が必要になる。長い距離を測るのは意外とやっかいなのだ（角度はそれよりずっと簡単だ）。

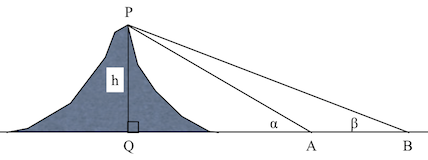
山までの距離がわらなくてもまったく問題ない。そのときは図2のように山と直線上に並ぶ2点、A、Bの2カ所から角度を測定する。ABの長さも測る。∠PAQ、∠PBQの大きさをそれぞれα、βとすると、

   

で求まる。

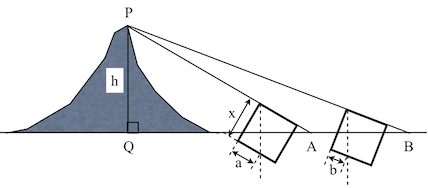
実はtanなんて使わない手法がある¹⁾。四方矩（シホウノカネ）という器具を使う。この器具は、各辺に長さの目盛が打たれた正方形の板の頂点の一つからおもり（下げ振り）がぶら下げられた器具。一辺を測りたい目標に向けて傾け、その時の糸の位置の目盛を読む。
図3で、正方形1辺の長さx、点Aでの目盛がa、点Bでの目盛がbだったとすると、山の高さ。

   

となる。すなわちtanをa/x、b/xで置き換えたもの。

この測り方はなかなかエレガントで好きだ。享保13年(1728)に書かれた松宮観山『分度余術』に載っている。考えついた人エライ。電卓も三角関数表も要らない。

上の方法は、山、点A、点Bが直線上に並んでいることが必要だ。この制約を取っ払いたければ正弦定理を使うことになる。

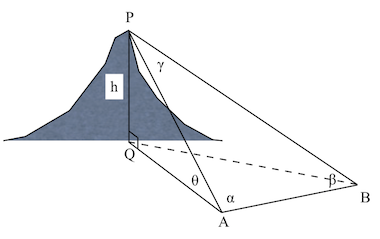
図4のように、離れた2点A、Bを決めてその間の長さを測る。このとき点A、点Bはどこでもよい。
∠PAB、∠ABP、∠QAPを測る。∠PAB、∠ABP、∠BPA、∠QAPの大きさをそれぞれα、β、γ、θとすると、

   

   

   

となる。

これらの方法に登場するのは三角形のみ。三角形は超スゴい図形なのだ。また、どの方法もちょっとやってみようかなと思えば手軽に試せるし（角度は分度器で、距離は歩幅かな）、もちろん確かな器具、技能で測れば精度は上がる。測定範囲が広くなると地球の丸みも考慮する。

幾何学的でわかりやすい高さはこれで測れるが、「標高」となるとややこしくなる。測地学の分野に突入してくるから。標高の定義は
標高=楕円体高-ジオイド高
とされる。楕円体高というのは地球を楕円体で近似した地球楕円体からの距離。ジオイド高というのは重力が等しい水準面（ジオイド）と楕円体高の差。要するに、標高は地表のある点とジオイドとの差ということ。ジオイドを求めるには重力を測る必要が出てくるし……。話はなかなか収まることなく、どんどんややこしい方向へと向かっていくのである。

プロたちはさらに精度を高めるため、日夜測定と計算を繰り返している。

＜参考文献＞
1) 国立国会図書館, コラム 測量の方法 江戸の数学

 - 測る